TP3 - Code de Huffman
Le codage de Huffman (1952) est une technique de compression de données permettant de stocker un message (un fichier) ou de le transmettre grâce à un minimum de bits afin d’améliorer les performances. Ce codage à taille variable suppose l’indépendance des caractères du message et on doit connaître la distribution probabiliste de ceux-ci à une position quelconque dans ce message. Plus la probabilité d’occurrence d’un caractère dans un fichier est grande, plus son code doit avoir une taille réduite.
On code chaque caractère par un mot de longueur variable de façon à ce qu’aucun mot ne soit le préfixe d’un autre. La propriété principale des codes de Huffman consiste en ce que la longueur moyenne du codage d’un caractère dans un fichier soit minimale.
Pour calculer le code d’un alphabet et de sa distribution, on construit un arbre binaire étiqueté par des 0 et des 1, les feuilles de cet arbre représentant les caractères tandis que les chemins issus de la racine constituent les codes correspondants.
Exemple 1
Soit l’alphabet a,b,c,d,e associé à la distribution probabiliste de la table 1.
| Caractère | a | b | c | d | e |
| Probabilité | 0,3 | 0,25 | 0,20 | 0,15 | 0,10 |
On obtient l’arbre binaire de Huffman de la figure 1. En parcourant cet arbre de la figure 1 on aboutit au code de Huffman correspondant à la table 2.
| Caractère | a | b | c | d | e |
| Code | 00 | 01 | 10 | 110 | 111 |
Table 2 – Code de Huffman
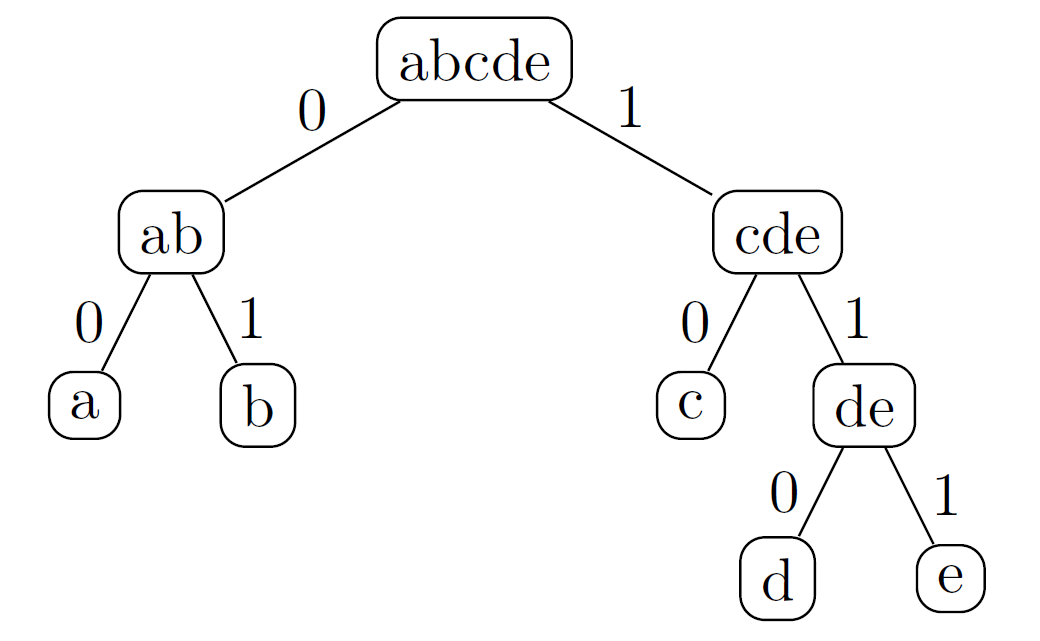
Remarquons que ce code n’est pas unique (il suffit de permuter les 0 et les 1). On calcule la longueur moyenne de codage comme suit :
- 75% des caractères nécessitent 2 bits (a,b,c) ;
- 25% des caractères nécessitent 3 bits (d,e) ;
- Lmoy = 75% * 2 + 25% * 3 = 2.25 bits
Remarquons qu’avec un code de taille fixe, chaque caractère aurait nécessité 3 bits, soit une perte de 33%.
3.1 Algorithme de Huffman
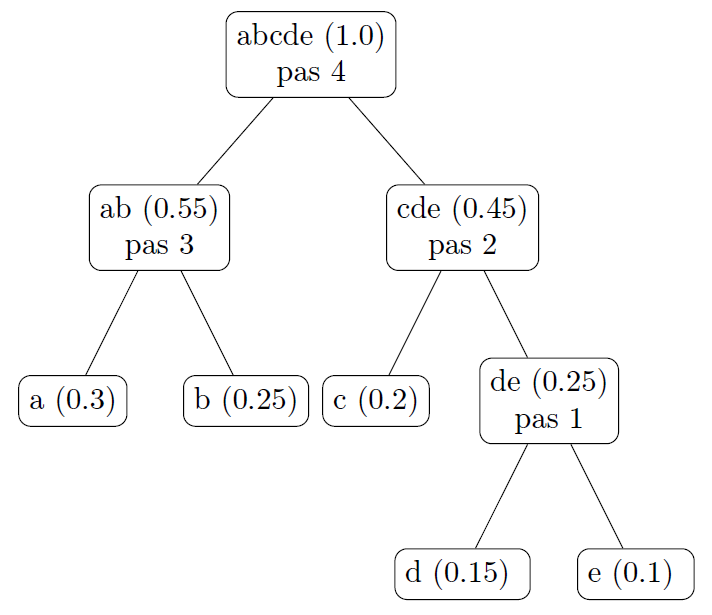
L’algorithme consiste à construire l’arbre en partant des deux feuilles “les plus basses” (plus faibles probabilités ici d et e). On leur associe un père, sorte de noeud virtuel dont la probabilité d’apparition du préfixe associé est égale à la somme des probabilités de ses deux fils. On réitère le processus en choisissant à nouveau les deux sommets sans père de plus faible probabilité jusqu’à la construction de la racine.
Exercice 14 (TD)
A l’aide de l’exemple précédent, construisez l’arbre de Huffman en précisant à chaque pas les noeuds créés.
Solution 14
Voir l’arbre de la figure 2.
Exercice 15 (TD/TP)
Soit la distribution probabiliste de la table 3 pour les dix caractères représentant les chiffres décimaux.
| Caractère | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Probabilité | 0,05 | 0,1 | 0,11 | 0,11 | 0,15 | 0,06 | 0,08 | 0,2 | 0,07 | 0,07 |
- Etablir manuellement un arbre de Huffman pour cette distribution en expliquant votre démarche.
- En utilisant le résultat précédent, établir le code de Huffman pour cette distribution de la table 3 en expliquant votre démarche.
- Donner la longueur moyenne de codage d’un chiffre du message.
Solution 15
-
Nous débuterons en étudiant les deux chiffres ayant les probabilités les plus faibles (0 et 5) et nous commencerons par construire le noeud 05 (0.11) en partant de ces deux feuilles “les plus basses”. Le père de 0 et de 5 constitue un noeud virtuel (référencé par 05) dont la probabilité d’apparition cumulée est égale à la somme des probabilités de ses deux fils, soit 0.11. Nous examinons maintenant les deux probabilités les plus faibles des autres chiffres et du nouveau noeud virtuel. De même que précédemment, nous formons un second noeud virtuel 89 dont la probabilité associée est de : 0.07 + 0.07 = 0.14
Nous recommençons avec les chiffres 1 et 6 et formons le nouveau noeud virtuel 16 de probabilité 0.18. Puis, nous faisons de même avec 2 et 3.
Arrivé à ce stade, les deux plus faibles probabilités appartiennent aux noeuds virtuels 05 et 89. Nous décidons donc de leur adjoindre un père 0589 ayant une probabilité de 0.11 + 0.14 = 0.25. Puis nous formons le père des noeuds 4 et 16 : 146 (0.33).
Nous continuons le même processus jusqu’à ce que l’on obtienne la racine de l’arbre qui est le noeud virtuel 0123456789 (1.0) dont la probabilité associée est 1. -
A ce moment, nous pouvons établir le code de Huffman de la table 4 associé à la distribution probabiliste donnée en parcourant l’arbre.
| Caractère | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Probabilité | 0,05 | 0,1 | 0,11 | 0,11 | 0,15 | 0,06 | 0,08 | 0,2 | 0,07 | 0,07 |
| Code | 1000 | 1111 | 010 | 011 | 110 | 1001 | 1110 | 00 | 1010 | 1011 |
- On peut vérifier que les codes les plus courts correspondent bien aux chiffres les plus fréquents : 7 (2 bits) ; 2,3,4 (3 bits). La longueur moyenne de codage est calculée de la façon suivante :
- 20% des chiffres nécessitent 2 bits (chiffre 7)
- 37% des chiffres nécessitent 3 bits (chiffres 2,3,4)
- 43% des chiffres nécessitent 4 bits (chiffres 0,1,5,6,8,9)
On a donc une longueur moyenne de codage d’un caractère égale à : Lmoy= 2*20% + 3*37% + 4*43%=3.23 bits/caractère.
Exercice 16 (TD/TP)
On souhaite calculer la distribution probabiliste des caractères d’un fichier passé en paramètre où les caractères sont stockés sur 8 bits.
- Décrire une structure de données à base de tableau permettant de calculer puis de stocker la distribution probabiliste.
- Ecrire l’algorithme pour calculer la distribution probabiliste.
- Ecrire le programme C correspondant.
Solution 16
Un tableau int compte[256] de 256 entiers initialisés à 0 nous parmettra de compter les
caractères. Puis un tableau float proba[256] de 256 flottants pour contenir la fréquence d’apparition.
Calcul des probabilités
taille=0
fic=ouvrir(argv[1])
TantQue EOF!=c=lireCar(fic)
compte[c]++
taille++
fermer(fic)
Pour i=0 à 255
proba[i]=compte[i]/taille
programme proba.c
#include <stdio.h>
#include <sys/types.h>
#include <sys/stat.h>
#include <fcntl.h>
#include <unistd.h>
/** Calcule la proba d’apparition des car dans le fichier chemin et remplit
* le tableau proba de taille 256
* @param chemin chaîne contenant le nom du fichier
* @param proba tableau de 256 flottants
* @return 0 si ok sinon erreur
*/
int calculProba(char *chemin, float *proba){
FILE* fic=fopen(chemin,"r");
if (!fic){
fprintf(stderr,"Impossible d’ouvrir le fichier %s !",chemin);
return 1; /* impossible ouvrir fichier */
}
int compte[256]={0};
int taille=0;
int c;
while(EOF!=(c=fgetc(fic))){
compte[c]++;
taille++;
}
fclose(fic);
if (taille==0)
return 0; /* fichier vide */
for(int i=0;i<256;i++){
proba[i]=compte[i]/(float)taille; // Attention un des deux doit être float!
// printf("DEBUG %f ",compte[i]/(float)taille);
}
return 0; /* OK */
}
int main(int argc, char *argv[], char *env[]) {
if (argc!=2){
printf("Syntaxe : %s fichier\n",argv[0]);
return 1; /* syntaxe */
}
float proba[256];
if (!calculProba(argv[1],proba)){ /* si O */
for(int i=0;i<256;i++){
if(proba[i]!=0){
printf("car : %c de code : %x de proba : %f\n",i,i,proba[i]);
}
}
return 0; /* OK */
}
return 2; /* calcul impossible */
}
Exercice 17 (TD/TP)
- Décrire une structure de données à base de tableau permettant de construire l’arbre de Huffman.
- Ecrire l’algorithme pour construire l’arbre ;
- Ecrire l’algorithme pour calculer le code de Huffman ; Huffman associé.
- On souhaite implémenter cet algorithme sur des fichiers où les caractères sont stockés sur 8 bits. Quelle est la taille minimale et maximale d’un code ? Comment stocker le tableau des codes dans le fichier codé ?
- (Projet) Programmer l’algorithme de compression et de décompression en C.
Solution 17
- Un tableau dont chaque ligne représente un noeud de l’arbre, dont les indices sont les chiffres (0-9), avec 4 colonnes contenant le père, le fils gauche, le fils droit, la proba du noeud. Nous utiliserons la structure de données schématisée dans la table 5 sous forme de tableau (fg signifie fils gauche tandis que fd signifie fils droit).
| indice | Pere | fg | fd | proba |
|---|---|---|---|---|
| 0 | -1 | -1 | -1 | 0,05 |
| 1 | -1 | -1 | -1 | 0,1 |
| 2 | -1 | -1 | -1 | 0,11 |
| 3 | -1 | -1 | -1 | 0,11 |
| 4 | -1 | -1 | -1 | 0,15 |
| 5 | -1 | -1 | -1 | 0,06 |
| 6 | -1 | -1 | -1 | 0,08 |
| 7 | -1 | -1 | -1 | 0,2 |
| 8 | -1 | -1 | -1 | 0,07 |
| 9 | -1 | -1 | -1 | 0,07 |
| 10 | -1 | -1 | -1 | -1 |
| 11 | -1 | -1 | -1 | -1 |
| 12 | -1 | -1 | -1 | -1 |
| 18 | -1 | -1 | -1 | -1 |
Table 5 – Structure de données
- Construction de l’arbre. L’objet de cet algorithme est de construire un arbre binaire complet. pour nouveau_noeud=10 à 18
- chercher i et j entre 0 et nouveau_noeud-1 tel que
- i = indice du noeud n’ayant pas de père (Pere=-1) et ayant la plus faible proba
- j = indice du noeud n’ayant pas de père (Pere=-1) et ayant la seconde plus faible proba
- // créer le nouveau noeud
ARBRE[nouveau_noeud,fg]=i; // on crèe l’arc fils gauche
ARBRE[nouveau_noeud,fd]=j; // on crèe l’arc fils droit
ARBRE[nouveau_noeud,proba]=ARBRE[i,proba]+ARBRE[j,proba]; // somme probas
ARBRE[i,pere]=nouveau_noeud; //on crèe l’arc pere
ARBRE[j,pere]=nouveau_noeud; //on crèe l’arc pere
end.
La phase 1) de cet algo. n’est pas détaillée car elle correspond à une simple recherche séquentielle des deux probabilités les plus faibles parmi les racines (noeuds sans père) de l’arbre en construction. La phase 1) permet de construire les arcs reliant le nouveau noeud virtuel à ses deux fils.
- Calcul du code. On va calculer le code d’un chiffre donné en parcourant l’arbre. Nous utiliserons le type chaîne de caractères pour former les codes des caractères. Cette version n’est pas efficace car on parcourt plusieurs fois les mêmes noeuds.
char* code[10] // codes des chiffres
Pour i=0 to 9
code[i]=""; // initialisation à chaîne vide
n=i;
TantQue ARBRE[n,pere] != -1 // tant que n n’est pas la racine
// concaténer (+) le code obtenu avec 0 ou 1
if ARBRE[ARBRE[n,pere], fg]=n // si n est le fils gauche de son père
code[i]=’0’+code[i]
else
code[i]=’1’+code[i];
n=ARBRE[n,pere]
Calcul du code (efficace) On partira de la racine et on fera une descente en profondeur à gauche à l’aide d’une fonction récursive : calculCode
fonction calculCode
Globales: nbcar : entier indiquant le nb de car différents du fichier;
pere, fg, fd : 3 tableaux de longueur 2*nbcar-1 réalisant le chaînage;
code : un tableau de chaînes de longueur nbcar
Données: noeud : indice du noeud;
buf : chaîne stockant le code en construction
Résultat:
début
si fg[noeud]=-1 alors // feuille
code[noeud]=buf
sinon
buf=buf + ’0’ // concaténation
calculCode(fg[noeud],buf)
buf=sous-chaine(buf,0,taille(buf)-2) // suppression du dernier car
buf=buf + ’1’ // concaténation
calculCode(fd[noeud],buf)
Cette fonction sera appelée par calculCode(2*nbcar-2,"")
- l’arbre le plus déséquilibré aura une profondeur de 255 donc la taille maxi de code sera de 255 bits tandis que la taille mini est de 1 bit. On peut stocker le tableau de code en en-tête du fichier.